命題25
もし、2つの数が互いに対して、立方数が立方数に対してもつ比をもち、初項が立方数ならば、そのとき、第2もまた立方数である。

2つの数AとBが互いに対して、立方数Cが立方数Dに対してもつ比をもつとし、Aを立方数とせよ。
Bもまた立方数であると主張する。
CとDは立方数で、CとDは相似な立体数なので、それゆえにCとDの間に2つの比例中項数がある。propositionⅧ19
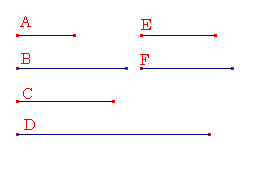
CとDの間と同じだけCとDと同じ比をもつ数の間に連続して比例する数があるので、それゆえに、AとBの間に2つの比例中項数EとFがある。propositionⅧ18
そのとき、A、E、F、Bは連続して比例し、Aは立方数なので、それゆえに、Bも立方数である。propositionⅧ23
それゆえに、もし、2つの数が互いに対して、立方数が立方数に対してもつ比をもち、初項が立方数ならば、そのとき、第2もまた立方数である。
証明終了